b站老王 自动驾驶决策规划学习记录(三)
算出一条满足约束的最优轨迹。什么是最优?平滑性舒适性尽可能短,耗时少约束:(1)轨迹连续性(2)无碰撞(3)交规(4)车辆动力学衡量轨迹质量往往用cost function表示sfta0a1ta5t5sfta0a1t...a5t5a0a1a5都是未知常数(a_{0},a_{1},...,a_{5}都是未知常数)a0a1...a5都是未知常数Jw1f˙2w2f¨2。
自动驾驶之凸优化和非凸优化
上一讲:b站老王 自动驾驶决策规划学习记录(二)
接着上一讲学习记录b站老王对自动驾驶规划系列的讲解
参考视频:自动驾驶决策规划算法第一章第二节 凸优化与非凸优化
0 前言
自动驾驶规划目标:算出一条满足约束的最优轨迹。
什么是最优?
指标:
- 平滑性
- 舒适性
- 尽可能短,耗时少
约束:(1)轨迹连续性(2)无碰撞(3)交规(4)车辆动力学
衡量轨迹质量往往用cost function表示
s = f ( t ) = a 0 + a 1 t + . . . + a 5 t 5 s = f(t)=a_{0}+a_{1}t+...+a_{5}t^5 s=f(t)=a0+a1t+...+a5t5 ( a 0 , a 1 , . . . , a 5 都是未知常数 ) (a_{0},a_{1},...,a_{5}都是未知常数) (a0,a1,...,a5都是未知常数)
cost function: J = w 1 f ˙ 2 + w 2 f ¨ 2 + w 3 f ( 3 ) 2 J = w_{1}\dot f^2+w_{2}\ddot f^2+w_{3}{f^{(3)}}^2 J=w1f˙2+w2f¨2+w3f(3)2
J J J越小,意味着越平滑,越舒适,当然也要满足各种约束。
1 求解高维复杂约束下的最小值问题
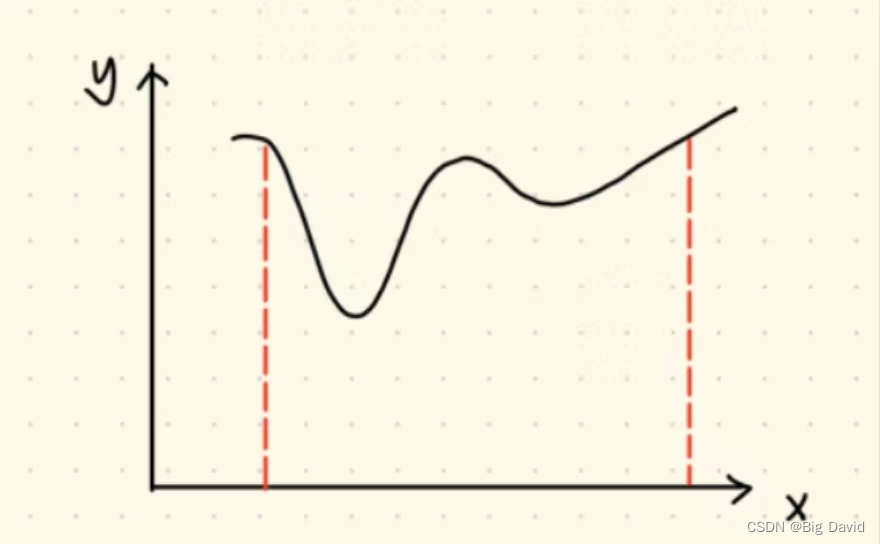
回忆:高中学过的求最小值方法
解 y = f ( x ) y = f(x) y=f(x)在 x ∈ [ a , b ] x∈[a,b] x∈[a,b]上的最小值( f ( x ) f(x) f(x)是连续可导函数)
- 算出 f ( a ) , f ( b ) f(a),f(b) f(a),f(b)
- 求 y ′ = f ′ ( x ) {y}' ={f}'(x) y′=f′(x)
- 令 y ′ = 0 {y}'=0 y′=0,解出 f ′ ( x ) = 0 {f}'(x)=0 f′(x)=0的根,设为 x 1 , x 2 , . . . , x n x_{1},x_{2},...,x_{n} x1,x2,...,xn
- 计算 f ( x 1 ) , f ( x 2 ) , . . . , f ( x n ) f(x_{1}),f(x_{2}),...,f(x_{n}) f(x1),f(x2),...,f(xn)与 f ( a ) , f ( b ) f(a),f(b) f(a),f(b)比较
此方法无法快速求解高维复杂约束下的最小值问题
y = l n s i n ( x + 1 x 2 ) + e c o s l n ( x 2 + 1 ) + x 5 + 1 x 2 + 6 y = lnsin(x+\frac{1}{x^2})+e^{cosln(x^2+1)}+x^5+\frac{1}{x^2+6} y=lnsin(x+x21)+ecosln(x2+1)+x5+x2+61
此函数求 d y d x \frac{dy}{dx} dxdy不难,但是求 d y d x = 0 \frac{dy}{dx}=0 dxdy=0较难。
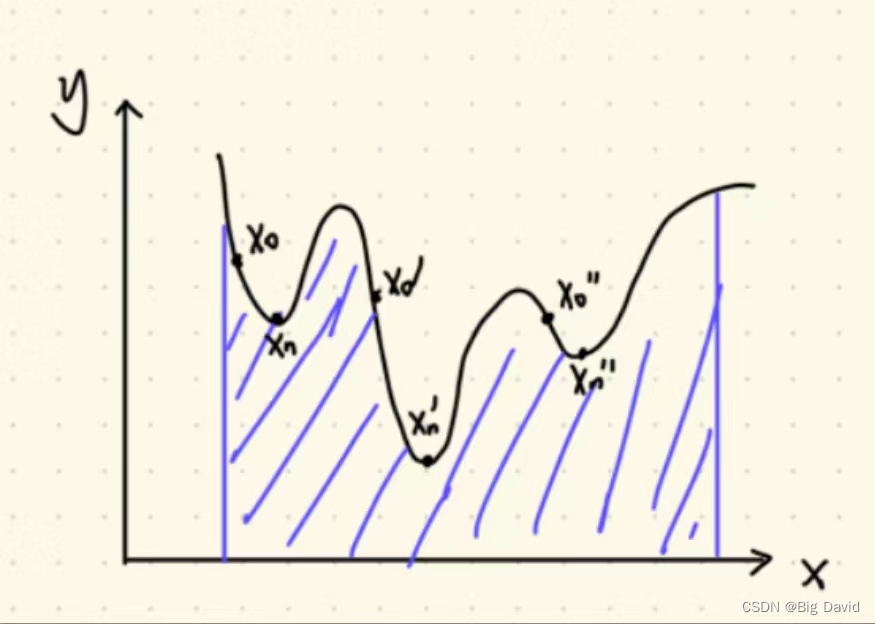
就算求出来极值点,但是看如下图所示的函数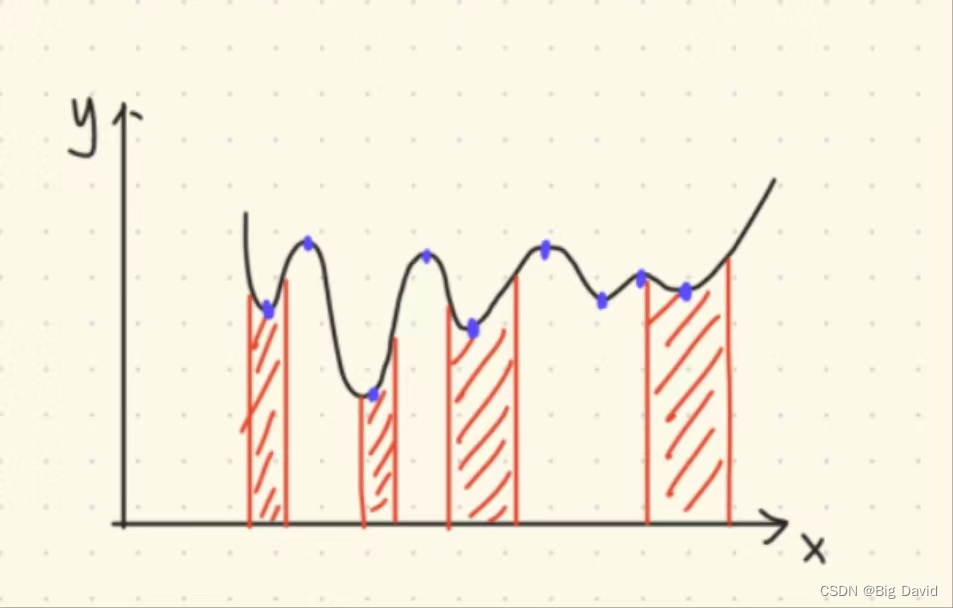
(1)极值点很多,难以快速计算
(2)约束复杂,是许多不连续小区间之并,处理较繁琐
一般求复杂函数在复杂约束下的最小值问题都采用
迭代法
- 牛顿法 (数值分析)
- 梯度下降法
- 高斯牛顿法(视觉slam十四讲)
1.1 梯度下降法
以梯度下降法为例,概述以下大概过程。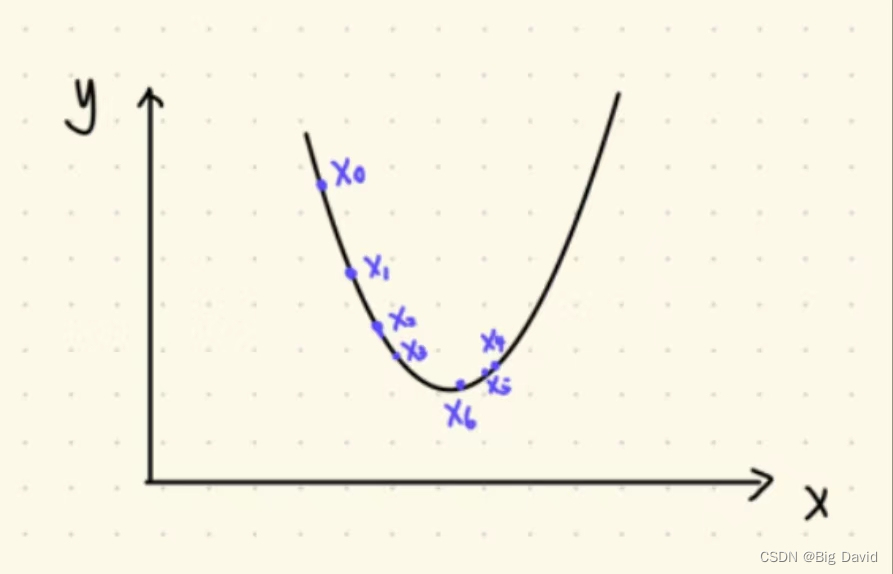
首先给定一个初值 x 0 x_{0} x0,根据初值的导数去判断下一步迭代的方向,(如果一元函数叫导数,多元函数叫梯度),按照梯度的反方向去迭代。如果导数为负,就往正方向迭代,导数为正,就往负方向迭代。如何收敛呢?迭代的过程不仅有方向,也有大小。大小就看导数的大小,导数大,收敛的大小也就越大。
详细讲梯度下降原理,大家可以看看这篇博客:【梯度下降法】详解优化算法之梯度下降法(原理、实现)
迭代法的缺点: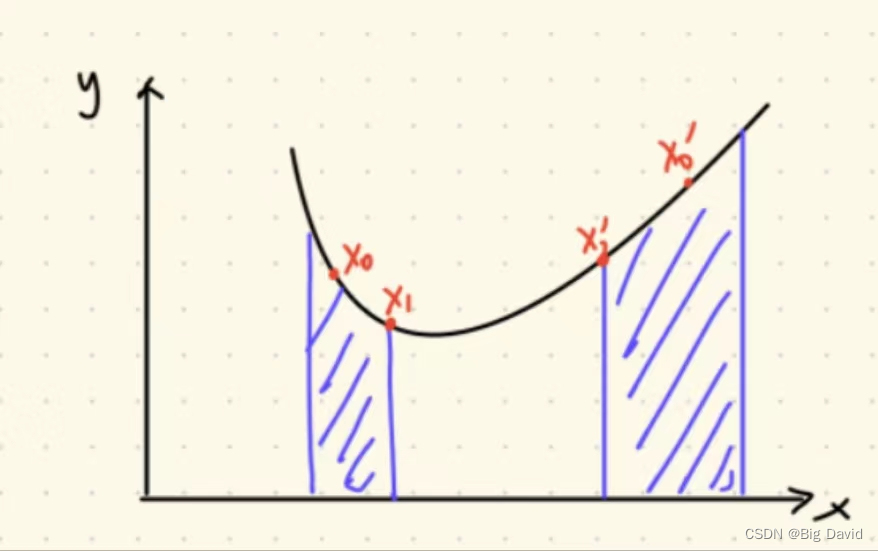
- 以 x 0 x_{0} x0为初值迭代,最终算法收敛于 x 1 x_{1} x1
- 以 x 0 ′ x_{0}' x0′为初值迭代,最终算法收敛于 x 1 ′ x_{1}' x1′
- 迭代法对初值敏感,有可能会收敛到局部极小值
2 凸优化
有一些性质较好的问题
(1)只有一个极值点,且为极小值点
(2)约束空间是一块“完整”的空间,不“破碎”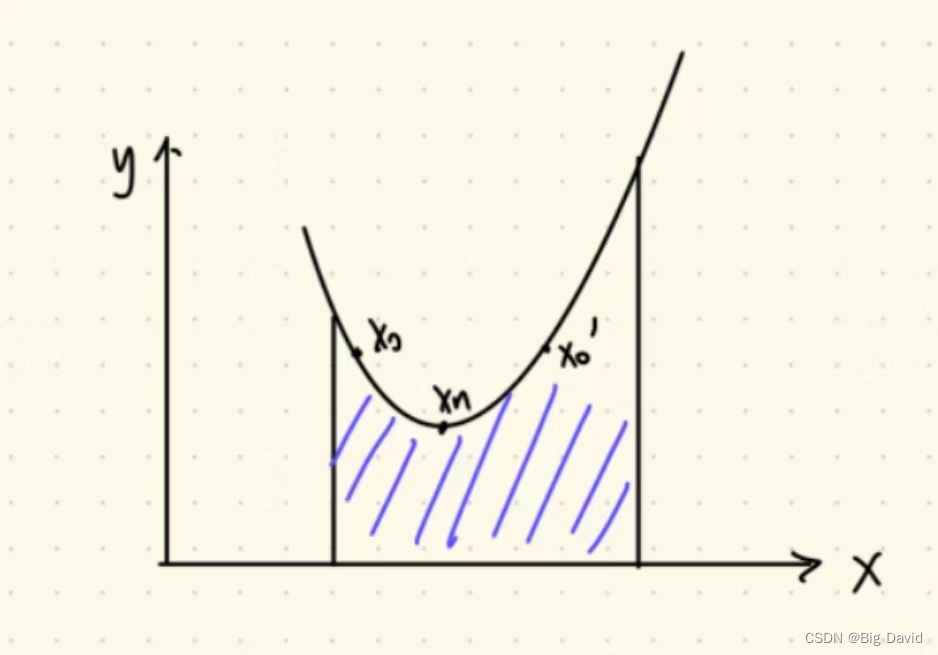
或者如下图所示的问题
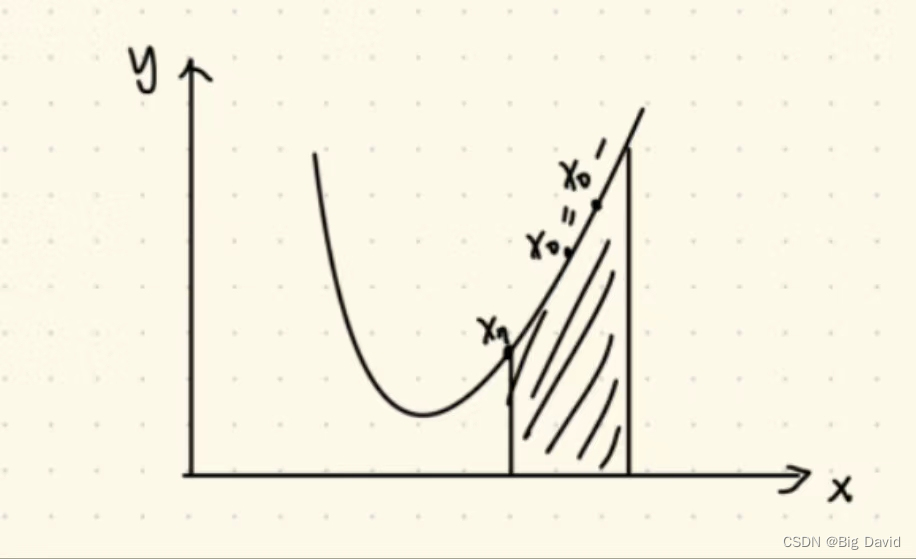
(1)没有极值点,在这个约束空间是单调的
(2)约束空间是一块“完整”的空间,不“破碎”
这类问题迭代法对初值不大敏感,且迭代法收敛的解必然是全局最小值。
这种好问题就叫做凸优化
凸优化必有两个性质:
- cost function只有一个极值点,且为极小值(不严谨,也可以是单调函数):凸函数
- 约束空间是一块“完整”、“不破碎”的空间 :凸空间
求凸函数在凸空间的最小值问题称为凸优化
凸空间的严谨定义,由凸多边形引申。左边的是凸多边形,右边的是凹多边形:
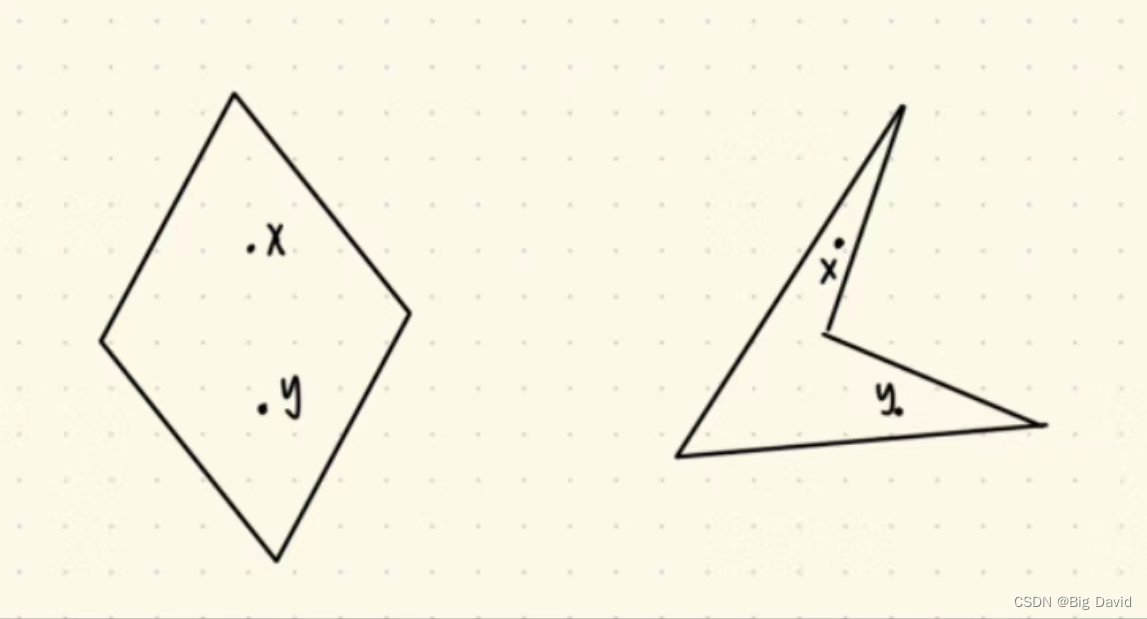
凸多边形定义,对于多边形内部 ∀ \forall ∀ 的点 x , y x,y x,y,都有 x + y 2 \frac{x+y}{2} 2x+y也在多边形内部,此多边形为凸多边形。
凹多边形定义, ∃ x , y \exists x,y ∃x,y ,使得 x + y 2 ∉ \frac{x+y}{2}\notin 2x+y∈/此多边形,此多边形为凹多边形。
下面来看一下凸空间和非凸空间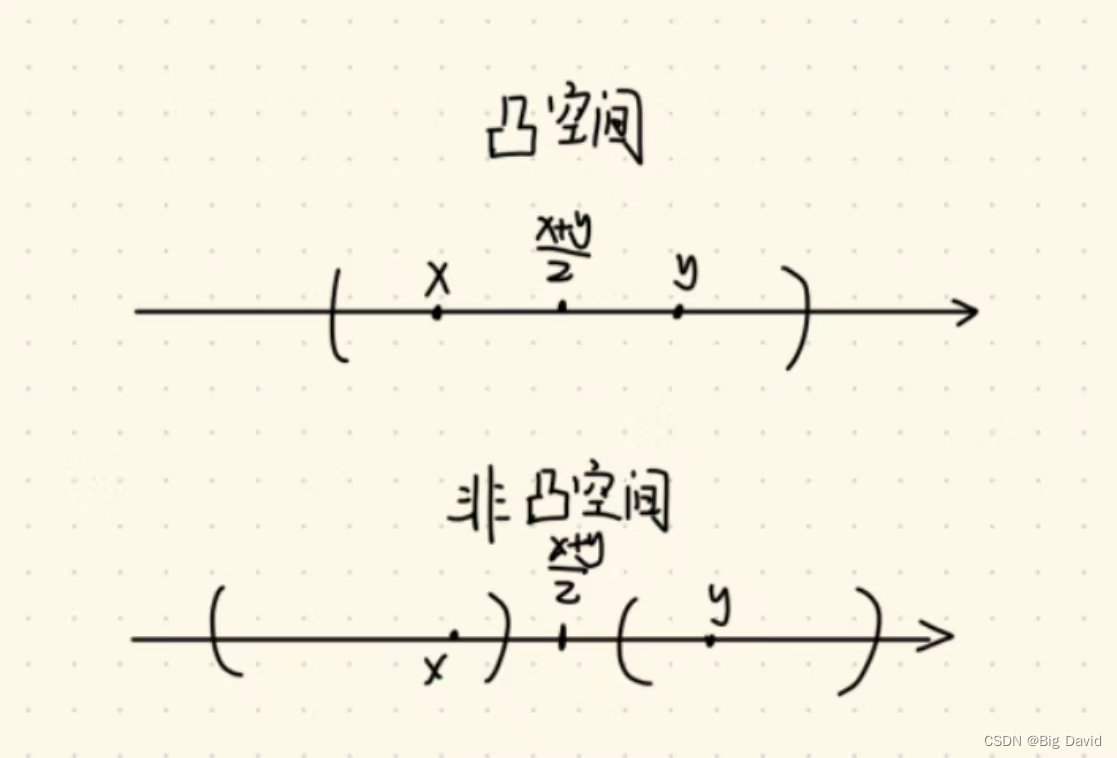
凸优化和自动驾驶之间的联系
问题:自动驾驶避障约束空间是不是凸空间?不是。
看下图
- 静态避障
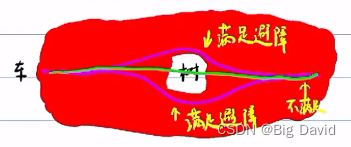
显然这是一个破碎的空间,车子可以从树的上面和下面绕开这颗树,但是上下除以二就不满足避障。
- 动态避障
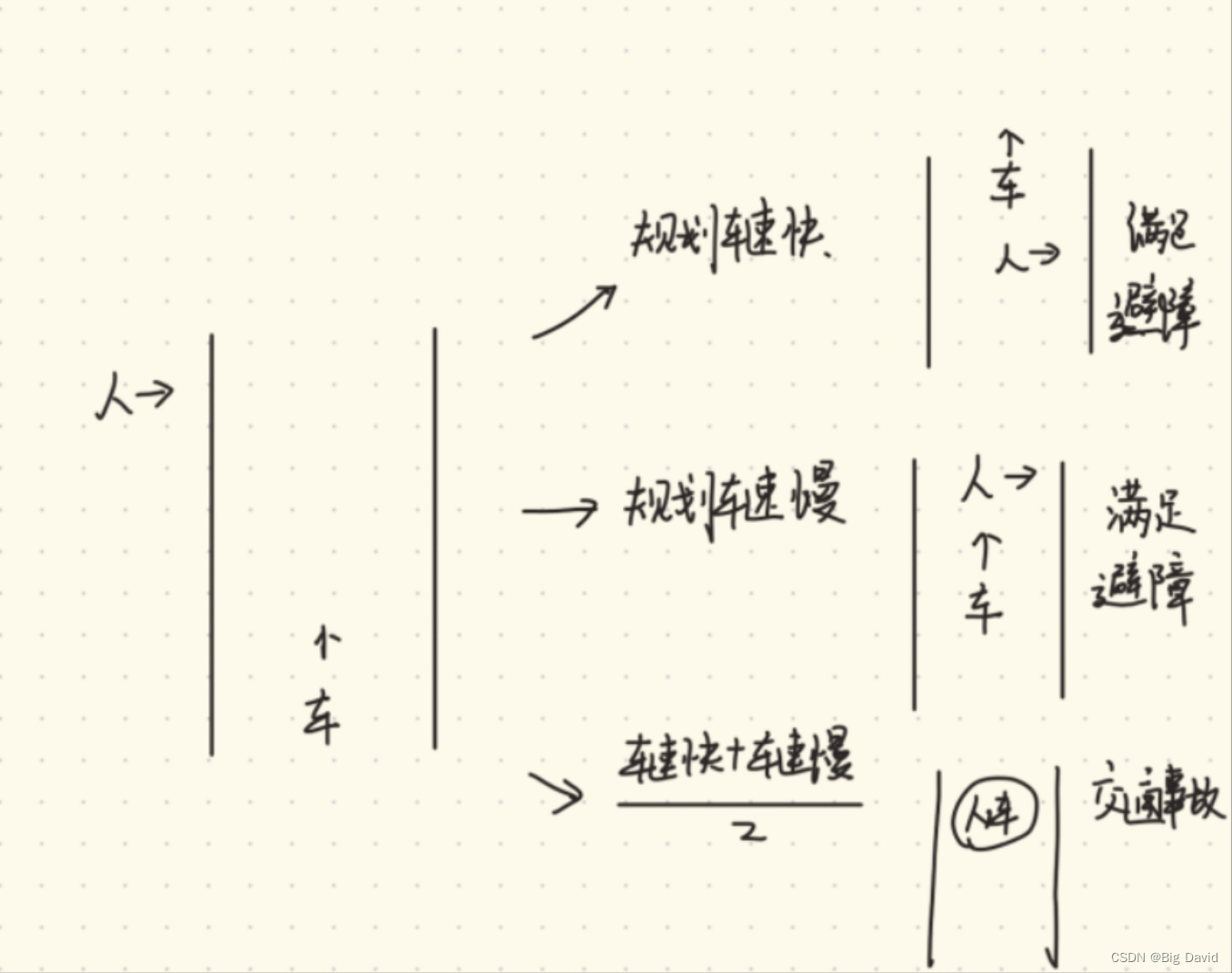
如上图所示三种情况,车规划的速度快,可以在人过马路的时候就已经在人的前面了;车规划的速度慢,可以在人过马路的时候及时停下来;但是(车速快+车速慢)/2就会导致车撞上人,发生交通事故。
静态+动态避障约束空间都不是凸的
如何求解非凸问题的最小值?
目前,并无完美的非凸问题算法
求解非凸问题的主要思路是找非凸问题中的凸结构
例如
(1)如下图所示函数是凸函数,但是约束空间是破碎的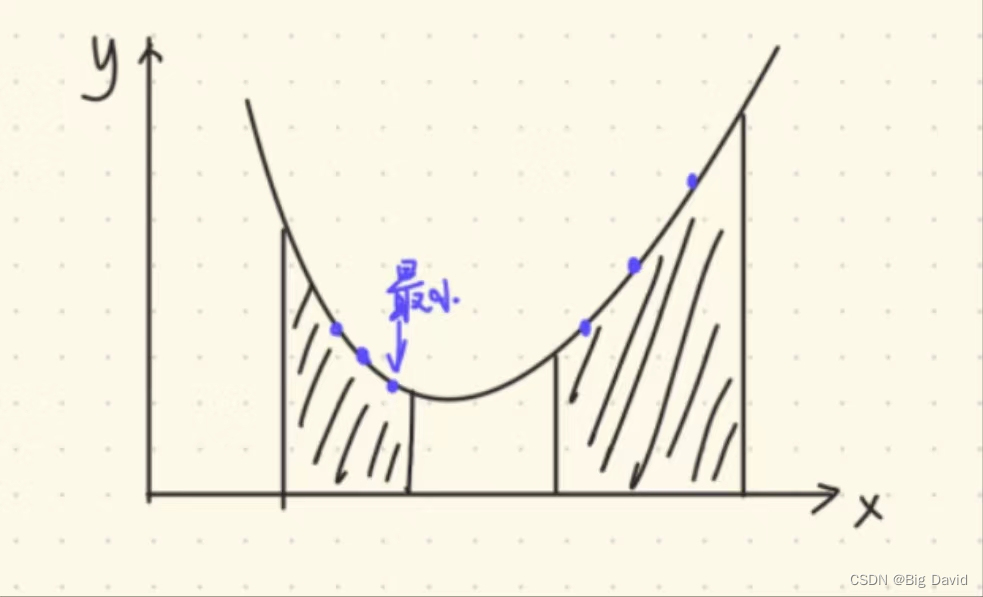
现在主流的算法是:启发式算法,先随机在约束空间采样一些离散的函数值,比大小,取最小的,作为迭代初值。
(2)对于非凸函数和非凸空间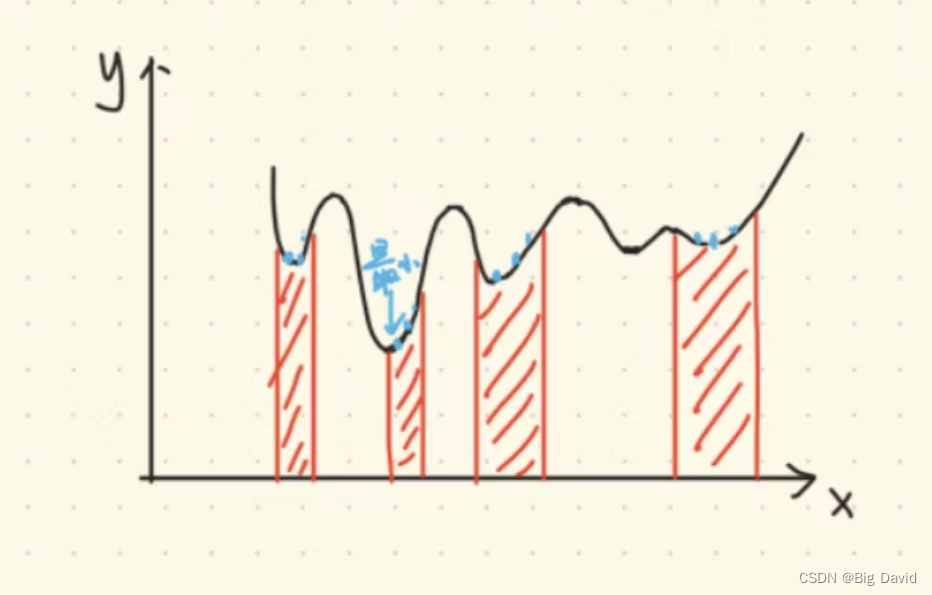
先在约束空间采样,找到采样点的最小值,本质上是连续空间离散化后,离散约束空间的最优解
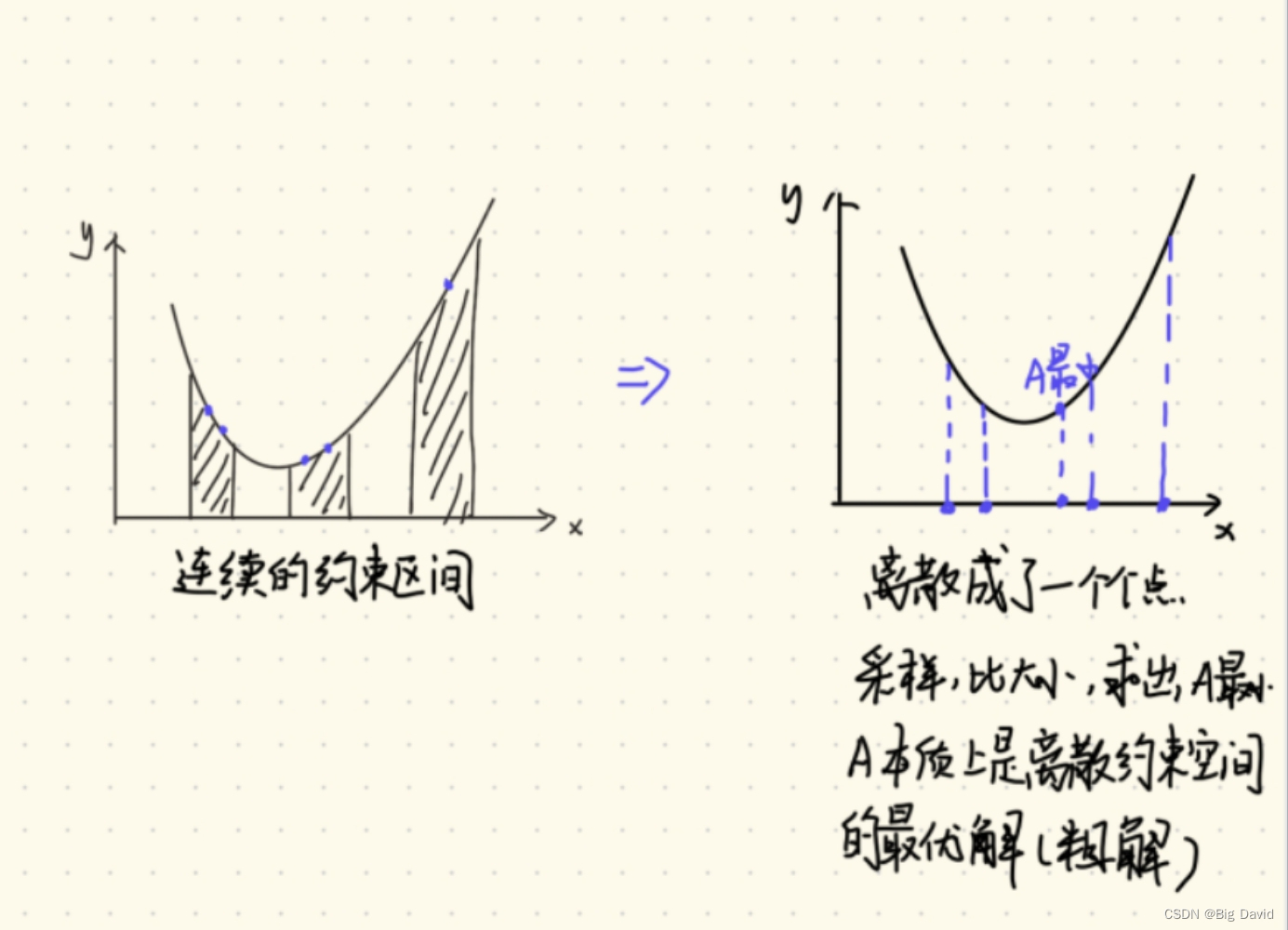
非凸空间 - > 离散化 -> 粗解(base) -> 迭代 -> 最终解
这种方法也不是尽善尽美的,如下图所示采样点较少
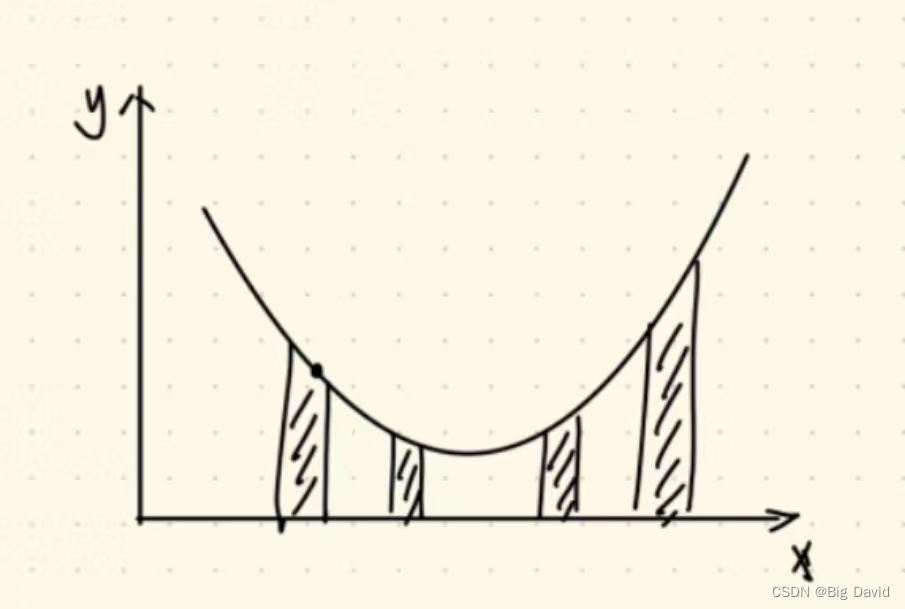
采样越少,越容易收敛到局部最优。
采样越多,容易发生维度灾难: 一维要采样100个点,二维要采样100*100 = 1w个点,三维可能要100w个点。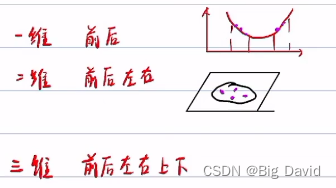
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容










所有评论(0)