SLAM文献之-RMS: Redundancy-Minimizing Point Cloud Sampling for Real-Time Pose Estimation
摘要——在移动机器人状态估计中常用的点云采样方法往往保留了大量的点冗余。这种冗余会不必要地减慢估计流程,并在实时约束下可能导致漂移。对于资源受限的机器人(特别是无人机)来说,这种延迟会成为瓶颈,而它们往往需要以极低的延迟实现敏捷且精准的操作。为此,我们提出了一种新颖的、确定性的、无需先验信息、仅含一个参数的点云采样方法,称为,该方法旨在最小化三维点云中的冗余。与现有方法不同,RMS 通过利用线性和
RMS(Redundancy-Minimizing Sampling)是一种专为实时姿态估计设计的点云采样算法,旨在减少点云中的冗余信息,提高估计效率和准确性。该方法通过最大化梯度流的熵来选择具有高信息量的点,从而优化点云的代表性。
文献摘要如下:
摘要——在移动机器人状态估计中常用的点云采样方法往往保留了大量的点冗余。这种冗余会不必要地减慢估计流程,并在实时约束下可能导致漂移。对于资源受限的机器人(特别是无人机)来说,这种延迟会成为瓶颈,而它们往往需要以极低的延迟实现敏捷且精准的操作。为此,我们提出了一种新颖的、确定性的、无需先验信息、仅含一个参数的点云采样方法,称为 RMS(Redundancy Minimization Sampling),该方法旨在最小化三维点云中的冗余。
与现有方法不同,RMS 通过利用线性和平面表面在迭代估计流程中固有的高冗余性,来平衡位移空间的可观测性。我们提出了“梯度流(gradient flow)”的概念,用于量化某点所处的局部表面信息。我们还证明,在机器人自运动估计中,最大化梯度流的熵可以有效最小化点的冗余。
我们将 RMS 集成到基于点的 KISS-ICP 和基于特征的 LOAM 里程计系统中,并在 KITTI、Hilti-Oxford 以及来自多旋翼无人机的自定义数据集上进行了实验评估。实验结果表明,在几何条件良好和退化的场景中,RMS 在运行速度、压缩率和估计精度方面均优于当前最先进的方法。
算法原理与流程
1. 梯度流(Gradient Flow)计算
对于点云中的每个点 ppp,RMS 计算其梯度流 Δp\Delta_pΔp,用于衡量该点在局部表面中的信息量。梯度流的计算基于点的局部邻域结构,为量化点的独特性(即未来生成非冗余残差的潜力),GFH 对于每个点 p∈Pp \in Pp∈P,在一个以 λp\lambda_pλp 为半径的球形邻域内寻找其邻居:
Np={j∣∥j−p∥2<λp, j=p, j∈P}(23) N_p = \{ j \mid \|j - p\|_2 < \lambda_p, \ j = p, \ j \in P \} \tag{23} Np={j∣∥j−p∥2<λp, j=p, j∈P}(23)
并定义梯度流(单位为米)为:
Δp=1∣Np∣∑j∈Np(j−p)(24) \Delta_p = \frac{1}{|N_p|} \sum_{j \in N_p} (j - p) \tag{24} Δp=∣Np∣1j∈Np∑(j−p)(24)
如图 所示,对于处于表面边界的点,GFH 分数较高;而对于表面内部的点(内点),GFH 分数较低。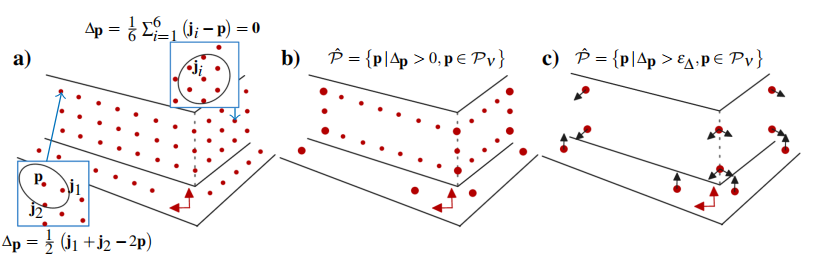
最大化 GFH 的结果是优先考虑表面边缘而不是内部点,这一点在以下两个方面尤为重要:
- 在点集 PPP 中,边缘点与对应物理表面边缘点匹配成功的潜力更大;
- 内部点可能产生错误的局部最小值,并在使用点对点度量时,阻碍沿超平面滑动的能力。
虽然点对超平面度量(point-to-hyperplane metrics)不易受到这个问题的影响(详见文献 [25]),但减少冗余仍有助于提升效率。
每种点集匹配算法在处理过程中或多或少都会对输入点集使用一个固定体素大小因子 ν\nuν 进行体素化,从而将原始点集 PPP 降采样为 Pν⊂PP_\nu \subset PPν⊂P。
利用这一点,在处理非结构化点集时设置邻域半径为:
λp=2ν \lambda_p = 2\nu λp=2ν
而在处理来自旋转式 3D LiDAR(如 Ouster) 的结构化点集时,邻域半径要考虑传感器的投影特性,定义为:
λp=2⋅max(ν,∥p∥2⋅max(sin2πC,sinθvR))(25) \lambda_p = 2 \cdot \max \left( \nu, \|p\|_2 \cdot \max\left( \sin \frac{2\pi}{C}, \sin \frac{\theta_v}{R} \right) \right) \tag{25} λp=2⋅max(ν,∥p∥2⋅max(sinC2π,sinRθv))(25)
其中:
- θv\theta_vθv:垂直视场角;
- 2π2\pi2π:水平视场角;
- RRR、CCC:对应结构化数据的行数和列数。
在以上方法中,邻域搜索(公式 23)是整个方法中计算量最大的部分。为了降低计算开销,从体素化后的点集 PνP_\nuPν 构建 KD 树。
- 使用 PνP_\nuPν 不仅降低了 KD 树的构建成本,
- 还减少了 KD 树查询的次数,仅为 ∣Pν∣|P_\nu|∣Pν∣。
2. 信息熵最大化采样
尽管冗余信息有助于降低噪声和离群点的影响,但它会使对应关系查找、残差生成、线性化和优化等迭代过程变得更加耗时。在存在终止条件的情形下,这种冗余甚至可能妨碍优化在合适时间内收敛。
为了解决公式(20)–(22)中定义的 NP-困难问题,我们可以将其建模为一个优化任务:
P^=argminΩ∈{Θ∣Θ⊆Pν,Θ≠∅}ΓΔ(Ω),subject to ∣Ω∣=NΩ(26) \hat{P} = \arg\min_{\Omega \in \{ \Theta \mid \Theta \subseteq P_\nu, \Theta \ne \emptyset \}} \Gamma_\Delta(\Omega), \quad \text{subject to } |\Omega| = N_\Omega \tag{26} P^=argΩ∈{Θ∣Θ⊆Pν,Θ=∅}minΓΔ(Ω),subject to ∣Ω∣=NΩ(26)
该优化目标是在给定输出点集数量 NΩ∈(1,∣Pν∣]N_\Omega \in (1, |P_\nu|]NΩ∈(1,∣Pν∣] 的约束下,最小化子集 Ω\OmegaΩ 中 GFH 流的冗余度 ΓΔ\Gamma_\DeltaΓΔ。
尽管固定输出数量是常见的设定(如 [2], [3]),但引入冗余度的概念可使问题形式更为严谨。由于最小化冗余等价于最大化信息熵,我们进一步提出其对偶形式:
P^=argmaxΩ∈{Θ∣Θ⊆Pν,Θ≠∅}HΔ(Ω),subject to HˉΔ(Ω)≤λHˉ(27) \hat{P} = \arg\max_{\Omega \in \{ \Theta \mid \Theta \subseteq P_\nu, \Theta \ne \emptyset \}} H_\Delta(\Omega), \quad \text{subject to } \bar{H}_\Delta(\Omega) \le \lambda_{\bar{H}} \tag{27} P^=argΩ∈{Θ∣Θ⊆Pν,Θ=∅}maxHΔ(Ω),subject to HˉΔ(Ω)≤λHˉ(27)
该形式在最大化 GFH 信息熵 HΔ(Ω)H_\Delta(\Omega)HΔ(Ω) 的同时,对相对熵速率 HˉΔ\bar{H}_\DeltaHˉΔ 设置终止阈值 λHˉ\lambda_{\bar{H}}λHˉ(百分比形式)。与固定输出数量的约束不同,这种终止准则可使选点过程自动适应点云的分布特性,从而具有环境无关性。引入适量冗余还能提升系统对噪声和异常值的鲁棒性。
令点集 Ω\OmegaΩ 的平均熵速率定义为:
μˉΔ(Ω)=1∣Ω∣HΔ(Ω)(28) \bar{\mu}_\Delta(\Omega) = \frac{1}{|\Omega|} H_\Delta(\Omega) \tag{28} μˉΔ(Ω)=∣Ω∣1HΔ(Ω)(28)
而信息熵为:
HΔ(Ω)=−∑p∈Ωp(Δp)logp(Δp)(29) H_\Delta(\Omega) = -\sum_{p \in \Omega} p(\Delta_p) \log p(\Delta_p) \tag{29} HΔ(Ω)=−p∈Ω∑p(Δp)logp(Δp)(29)
其中 p(Δp)p(\Delta_p)p(Δp) 是观测到 GFH 值 Δp\Delta_pΔp 的概率。
相对熵速率为归一化形式:
HˉΔ(Ω)=μˉΔ(Ω)μˉΔ∗(Ω)(30) \bar{H}_\Delta(\Omega) = \frac{\bar{\mu}_\Delta(\Omega)}{\bar{\mu}_\Delta^*(\Omega)} \tag{30} HˉΔ(Ω)=μˉΔ∗(Ω)μˉΔ(Ω)(30)
其中:
μˉΔ∗(Ω)=maxΨ∈{Θ∣Θ⊆Ω,Θ≠∅}μˉΔ(Ψ)(31) \bar{\mu}_\Delta^*(\Omega) = \max_{\Psi \in \{ \Theta \mid \Theta \subseteq \Omega, \Theta \ne \emptyset \}} \bar{\mu}_\Delta(\Psi) \tag{31} μˉΔ∗(Ω)=Ψ∈{Θ∣Θ⊆Ω,Θ=∅}maxμˉΔ(Ψ)(31)
代表所有非空子集中的最大平均熵速率。由于熵速率与数据冗余呈反比关系,因此可以使用最大化熵作为消除冗余的对偶优化目标。
由于概率函数 ppp 随点云环境 PνP_\nuPν 而变化,无法建模为标准的概率密度函数,因此采用频率估计法近似概率分布:
- 首先将所有点的 GFH 向量范数归一化:
ΔˉPν={∣∣Δp∣∣2max∣∣ΔPν∣∣2 | p∈Pν}(32) \bar{\Delta}_{P_\nu} = \left\{ \frac{||\Delta_p||_2}{\max ||\Delta_{P_\nu}||_2} \,\middle|\, p \in P_\nu \right\} \tag{32} ΔˉPν={max∣∣ΔPν∣∣2∣∣Δp∣∣2 p∈Pν}(32)
-
在区间 [0, 1] 上将归一化值划分为 KKK 个直方图 bin,得到 GFH 的直方图 HΔH_\DeltaHΔ。每个 bin k∈{1,…,K}k \in \{1, \dots, K\}k∈{1,…,K} 包含一个点集 HΔk\mathcal{H}_\Delta^kHΔk。
-
每个 bin 的概率为:
pk=∣HΔk∣∣Pν∣ p_k = \frac{|\mathcal{H}_\Delta^k|}{|P_\nu|} pk=∣Pν∣∣HΔk∣
算法 1:基于 GFH 熵的采样方法(伪代码概述)
该方法依照公式(27)进行点采样:
- 构建空直方图 H^Δ\hat{H}_\DeltaH^Δ
- 在 HΔH_\DeltaHΔ 中逐 bin 从高到低轮流采样,将每个 bin 中一个点移入 H^Δ\hat{H}_\DeltaH^Δ
- 主排序键:选取 bin 中 GFH 值最大的点
次排序键:点的欧式范数最大(用于提升旋转约束能力)
pk=argmaxp∈HΔkΔp,pk′=argmaxp∈HΔk∣∣p∣∣2(33) p_k = \arg\max_{p \in \mathcal{H}_\Delta^k} \Delta_p, \quad p_k' = \arg\max_{p \in \mathcal{H}_\Delta^k} ||p||_2 \tag{33} pk=argp∈HΔkmaxΔp,pk′=argp∈HΔkmax∣∣p∣∣2(33)
这种做法兼顾了 GFH 分布的均匀性和点在残差中可能带来的旋转观测价值。
终止准则与最终样本集
- 每轮采样后,若满足 Eq. (27) 的终止条件,或采样轮数 i≥Ki \ge Ki≥K(最大步数),则采样结束。
- 因为熵在 KKK 次迭代内达到最大值,所以 Eq. (31) 可重写为:
μˉΔ∗(Pν)=maxi=1,…,KμˉΔ(P^i)(34) \bar{\mu}_\Delta^*(P_\nu) = \max_{i = 1,\dots,K} \bar{\mu}_\Delta(\hat{P}_i) \tag{34} μˉΔ∗(Pν)=i=1,…,KmaxμˉΔ(P^i)(34)
其中 P^i\hat{P}_iP^i 是第 iii 轮时采样得到的点集。
最终采样结果为所有迭代中收集到的点:
P^=P^i \hat{P} = \hat{P}_i P^=P^i
小结与优势
这种基于 GFH 的熵最大化采样方法实现了以下目标:
- 消除冗余,提升效率
- 保留一定空间分布结构(类似体素化效果)
- 对噪声与异常值更具鲁棒性
- 优于直接累计 GFH 的贪心策略,避免欠约束问题
它为后续配准和优化流程提供了更具信息价值的点集输入,有助于增强估计精度并提升整体计算效率。
3. 次要关键字选择
在梯度流相近的情况下,RMS 使用点的范数 ∥p∥\|p\|∥p∥ 作为次要关键字,优先选择距离原点较远的点,以增强旋转空间的可观测性。
4. 整体算法流程

主要创新点
- 信息驱动的采样策略:通过最大化梯度流的熵,RMS 有效减少了冗余点,提高了姿态估计的效率和准确性。
- 单参数控制:仅需设置体素大小 ν\nuν,简化了参数调优过程。
- 与现有系统的兼容性:RMS 可无缝集成到现有的姿态估计系统中,如 KISS-ICP 和 LOAM。
- 适应退化环境:在几何结构退化的环境中,RMS 仍能保持良好的估计性能。
应用与实验验证
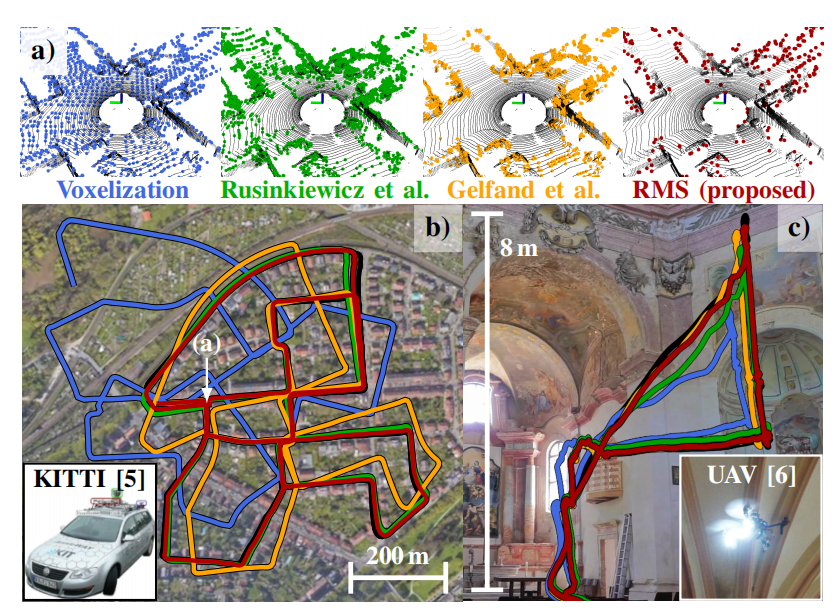
RMS 已在多个数据集上进行了验证,包括 KITTI、Hilti-Oxford 以及多旋翼无人机采集的自定义数据集。实验结果表明,RMS 在速度、压缩率和估计精度方面均优于现有的采样方法,特别是在几何结构退化的场景中表现突出。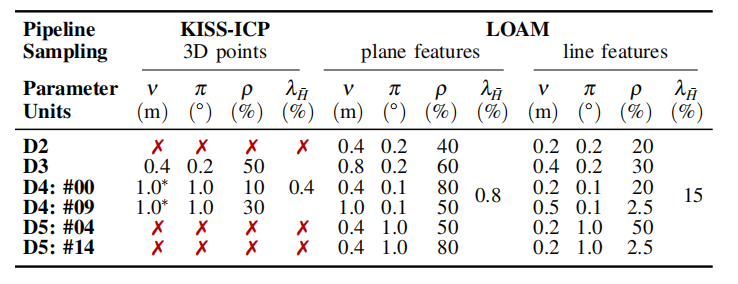
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)